BRASAMCAN YN EXCEL

Send

Ymhlith y gwahanol ddulliau rhagweld, ni all un ddim ond brasamcanu'r brasamcan. Gan ei ddefnyddio, gallwch wneud amcangyfrifon bras a chyfrifo'r dangosyddion a gynlluniwyd trwy ddisodli'r gwrthrychau gwreiddiol gyda rhai symlach. Yn Excel, mae posibilrwydd hefyd o ddefnyddio'r dull hwn ar gyfer rhagweld a dadansoddi. Gadewch i ni edrych ar sut y gellir defnyddio'r dull hwn yn y rhaglen benodol gydag offer adeiledig.

Brasamcan

Daw enw'r dull hwn o'r gair Lladin proxima - “agosaf”. Mae'n frasamcanu trwy symleiddio a llyfnhau dangosyddion hysbys, gan eu hadeiladu i mewn i duedd sy'n sail iddo. Ond gellir defnyddio'r dull hwn nid yn unig ar gyfer rhagweld, ond hefyd ar gyfer astudio canlyniadau sy'n bodoli eisoes. Wedi'r cyfan, brasamcan, mewn gwirionedd, yw symleiddio'r data ffynhonnell, ac mae'n haws archwilio fersiwn wedi'i symleiddio.

Y prif offeryn ar gyfer llyfnhau yn Excel yw adeiladu llinell duedd. Y gwir yw, ar sail y dangosyddion presennol, bod graff swyddogaeth ar gyfer cyfnodau yn y dyfodol yn cael ei gwblhau. Prif bwrpas y llinell duedd, fel y gallech ddyfalu, yw gwneud rhagolygon neu nodi tuedd gyffredinol.

Ond gellir ei adeiladu gan ddefnyddio un o bum math o frasamcan:

Llinol;
Esbonyddol;
Logarithmig;
Polynomial;
Pwer.

Rydym yn ystyried pob un o'r opsiynau yn fwy manwl ar wahân.

Gwers: Sut i adeiladu llinell duedd yn Excel

Dull 1: llyfnhau llinol

Yn gyntaf oll, gadewch inni edrych ar yr opsiwn brasamcan symlaf, sef defnyddio swyddogaeth linellol. Byddwn yn canolbwyntio arno'n fwy manwl, gan y byddwn yn amlinellu'r pwyntiau cyffredinol sy'n nodweddiadol o ddulliau eraill, sef, llunio amserlen a rhai naws eraill na fyddwn yn dibynnu arnynt wrth ystyried yr opsiynau canlynol.

Yn gyntaf oll, byddwn yn adeiladu graff, y byddwn yn cyflawni'r weithdrefn llyfnhau ar ei sail. I adeiladu amserlen, rydym yn cymryd tabl lle nodir cost fisol uned gynhyrchu a gynhyrchir gan y fenter a'r elw cyfatebol mewn cyfnod penodol. Bydd y swyddogaeth graffig y byddwn yn ei hadeiladu yn adlewyrchu dibyniaeth y cynnydd mewn elw ar y gostyngiad yng nghost cynhyrchu.

I blotio, yn gyntaf oll, dewiswch y colofnau "Cost Uned" a Elw. Ar ôl hynny, symudwch i'r tab Mewnosod. Nesaf, ar y rhuban yn y blwch offer Siartiau, cliciwch ar y botwm "Spot". Yn y rhestr sy'n agor, dewiswch yr enw "Spot gyda chromliniau a marcwyr llyfn". Y math hwn o siart sydd fwyaf addas ar gyfer gweithio gyda llinell duedd, ac felly, ar gyfer defnyddio'r dull brasamcanu yn Excel.

Mae'r amserlen wedi'i hadeiladu.

I ychwanegu llinell duedd, dewiswch hi trwy glicio botwm dde'r llygoden. Mae dewislen cyd-destun yn ymddangos. Dewiswch yr eitem ynddo "Ychwanegu llinell duedd ...".
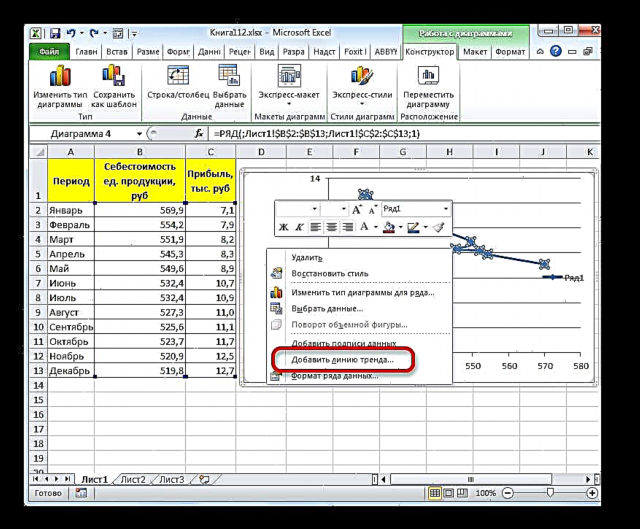
Mae yna opsiwn arall i'w ychwanegu. Mewn grŵp ychwanegol o dabiau ar y rhuban "Gweithio gyda siartiau" symud i'r tab "Cynllun". Ymhellach yn y bloc offer "Dadansoddiad" cliciwch ar y botwm Llinell Tueddiadau. Mae'r rhestr yn agor. Gan fod angen i ni gymhwyso brasamcan llinol, rydym yn dewis o'r swyddi a gyflwynir "Brasamcan llinol".

Serch hynny, os dewisoch chi'r opsiwn cyntaf gydag ychwanegu gweithredoedd trwy'r ddewislen cyd-destun, bydd ffenestr fformat yn agor.
Yn y bloc o baramedrau "Adeiladu llinell duedd (brasamcanu a llyfnhau)" gosod y switsh i'w safle "Llinol".
Os dymunir, gallwch wirio'r blwch wrth ymyl y safle "Dangos hafaliad yn y diagram". Ar ôl hynny, bydd hafaliad y swyddogaeth llyfnhau yn cael ei arddangos ar y diagram.
Hefyd yn ein hachos ni, er mwyn cymharu gwahanol opsiynau brasamcan, mae'n bwysig gwirio'r blwch nesaf at "Rhowch ar y siart werth brasamcan dibynadwy (R ^ 2)". Gall y dangosydd hwn amrywio o 0 o'r blaen 1. Po uchaf ydyw, mae'r brasamcan yn well (yn fwy dibynadwy). Credir, gyda gwerth y dangosydd hwn 0,85 ac yn uwch, gellir ystyried llyfnhau yn ddibynadwy, ond os yw'r dangosydd yn is, yna na.
Ar ôl cwblhau pob un o'r gosodiadau uchod. Cliciwch ar y botwm Caewchwedi'i leoli ar waelod y ffenestr.

Fel y gallwch weld, mae'r llinell duedd yn cael ei chynllwynio ar y siart. Gyda brasamcan llinol, fe'i nodir gan linell syth ddu. Gellir defnyddio'r math penodedig o lyfnhau yn yr achosion symlaf pan fydd y data'n newid yn eithaf cyflym ac mae dibyniaeth gwerth swyddogaeth ar y ddadl yn amlwg.

Disgrifir y llyfnhau a ddefnyddir yn yr achos hwn gan y fformiwla ganlynol:

y = bwyell + b

Yn ein hachos ni ni, mae'r fformiwla ar y ffurf ganlynol:

y = -0.1156x + 72.255

Mae gwerth cywirdeb brasamcan yn hafal i 0,9418, sy'n ganlyniad eithaf derbyniol sy'n nodweddu llyfnhau fel dibynadwy.

Dull 2: Brasamcan Esbonyddol

Nawr, gadewch i ni edrych ar y math esbonyddol o frasamcan yn Excel.

Er mwyn newid math y llinell duedd, dewiswch hi trwy glicio botwm dde'r llygoden a dewis yr eitem yn y ddewislen naidlen "Fformat y llinell duedd ...".

Ar ôl hynny, mae'r ffenestr fformat cyfarwydd yn cychwyn. Yn y bloc dewis math brasamcanu, gosodwch y switsh i "Esbonyddol". Bydd y gosodiadau sy'n weddill yn aros yr un fath ag yn yr achos cyntaf. Cliciwch ar y botwm Caewch.

Ar ôl hynny, bydd y llinell duedd yn cael ei chynllwynio ar y siart. Fel y gallwch weld, wrth ddefnyddio'r dull hwn, mae ganddo siâp ychydig yn grwm. Yn yr achos hwn, mae'r lefel hyder yn 0,9592, sy'n uwch nag wrth ddefnyddio brasamcan llinol. Defnyddir y dull esbonyddol orau pan fydd y gwerthoedd yn newid yn gyflym yn gyflym ac yna'n cymryd ffurf gytbwys.

Mae ffurf gyffredinol y swyddogaeth llyfnhau fel a ganlyn:

y = be ^ x

lle e yw sylfaen y logarithm naturiol.

Yn ein hachos ni ni, roedd y fformiwla ar y ffurf ganlynol:

y = 6282.7 * e ^ (- 0.012 * x)

Dull 3: llyfnhau logarithmig

Nawr mae'n dro i ystyried y dull o frasamcanu logarithmig.

Yn yr un modd â'r amser blaenorol, rydym yn lansio'r ffenestr fformat llinell duedd trwy'r ddewislen cyd-destun. Gosodwch y switsh i'w safle "Logarithmig" a chlicio ar y botwm Caewch.

Mae gweithdrefn ar gyfer adeiladu llinell duedd gyda brasamcan logarithmig. Fel yn yr achos blaenorol, mae'n well defnyddio'r opsiwn hwn pan fydd y data'n newid yn gyflym i ddechrau ac yna'n edrych yn gytbwys. Fel y gallwch weld, y lefel hyder yw 0.946. Mae hyn yn uwch na defnyddio'r dull llinellol, ond yn is nag ansawdd y llinell duedd gyda llyfnhau esbonyddol.

Yn gyffredinol, mae'r fformiwla llyfnhau yn edrych fel hyn:

y = a * ln (x) + b

lle ln yw gwerth y logarithm naturiol. Felly enw'r dull.

Yn ein hachos ni, mae'r fformiwla ar y ffurf ganlynol:

y = -62.81ln (x) +404.96

Dull 4: llyfnhau polynomial

Mae'r amser wedi dod i ystyried y dull o lyfnhau polynomial.

Ewch i ffenestr fformat y llinell duedd, fel y gwnaed fwy nag unwaith. Mewn bloc "Adeiladu llinell duedd" gosod y switsh i'w safle "Polynomial". I'r dde o'r eitem hon mae maes "Gradd". Wrth ddewis gwerth "Polynomial" mae'n dod yn weithredol. Yma gallwch nodi unrhyw werth pŵer o 2 (wedi'i osod yn ddiofyn) i 6. Mae'r dangosydd hwn yn pennu nifer uchafsymiau a lleiafswm y swyddogaeth. Wrth osod polynomial o'r ail radd, dim ond un uchafswm sy'n cael ei ddisgrifio, ac wrth osod polynomial o'r chweched radd, gellir disgrifio hyd at bum uchafswm. Yn gyntaf, gadewch inni adael y gosodiadau diofyn, hynny yw, byddwn yn nodi'r ail radd. Rydyn ni'n gadael gweddill y gosodiadau yr un peth ag y gwnaethon ni eu gosod yn y dulliau blaenorol. Cliciwch ar y botwm Caewch.

Mae'r llinell duedd sy'n defnyddio'r dull hwn yn cael ei blotio. Fel y gallwch weld, mae hyd yn oed yn fwy crwm nag wrth ddefnyddio brasamcan esbonyddol. Mae'r lefel hyder yn uwch na gydag unrhyw un o'r dulliau a ddefnyddiwyd o'r blaen, ac mae'n 0,9724.
Gellir defnyddio'r dull hwn yn fwyaf llwyddiannus os yw'r data'n newidiol yn gyson. Mae'r swyddogaeth sy'n disgrifio'r math hwn o lyfnhau yn edrych fel hyn:
y = a1 + a1 * x + a2 * x ^ 2 + ... + an * x ^ n
Yn ein hachos ni, roedd y fformiwla ar y ffurf ganlynol:
y = 0.0015 * x ^ 2-1.7202 * x + 507.01
Nawr, gadewch i ni newid graddfa'r polynomials i weld a fydd y canlyniad yn wahanol. Dychwelwn i'r ffenestr fformat. Rydym yn gadael y math brasamcanu polynomial, ond gyferbyn ag ef, yn ffenestr y radd, yn gosod y gwerth mwyaf posibl - 6.

Fel y gallwch weld, ar ôl hyn roedd ein llinell duedd ar ffurf cromlin amlwg, lle mae nifer yr uchafsymiau yn chwech. Cynyddodd y lefel hyder hyd yn oed yn fwy, gan ddod i gyfanswm 0,9844.

Mae'r fformiwla sy'n disgrifio'r math hwn o lyfnhau ar y ffurf ganlynol:

y = 8E-08x ^ 6-0,0003x ^ 5 + 0,3725x ^ 4-269,33x ^ 3 + 109525x ^ 2-2E + 07x + 2E + 09

Dull 5: llyfnhau pŵer

I gloi, rydym yn ystyried y dull brasamcanu cyfraith pŵer yn Excel.

Rydym yn symud i'r ffenestr Fformat Llinell Tuedd. Gosodwch y math o switsh llyfnhau i'w safle "Pwer". Mae arddangos yr hafaliad a lefel yr hyder, fel bob amser, yn cael ei adael ymlaen. Cliciwch ar y botwm Caewch.

Mae'r rhaglen yn ffurfio llinell duedd. Fel y gallwch weld, yn ein hachos ni mae'n llinell gyda tro bach. Mae'r lefel hyder yn 0,9618, sy'n gyfradd eithaf uchel. O'r holl ddulliau uchod, roedd y lefel hyder yn uwch yn unig wrth ddefnyddio'r dull polynomial.

Defnyddir y dull hwn yn effeithiol mewn achosion o newid data swyddogaeth yn ddwys. Mae'n bwysig ystyried bod yr opsiwn hwn yn berthnasol dim ond o dan yr amod nad yw'r swyddogaeth a'r ddadl yn derbyn gwerthoedd negyddol neu sero.

Mae gan y fformiwla gyffredinol sy'n disgrifio'r dull hwn y ffurf ganlynol:

y = bx ^ n

Yn ein hachos ni ni, mae'n edrych fel hyn:

y = 6E + 18x ^ (- 6.512)

Fel y gallwch weld, wrth ddefnyddio'r data penodol a ddefnyddiwyd gennym fel enghraifft, dangosodd y dull o frasamcanu polynomial â pholynomial i'r chweched radd y lefel uchaf o ddibynadwyedd (0,9844), y lefel isaf o hyder yn y dull llinellol (0,9418) Ond nid yw hyn yn golygu o gwbl y bydd yr un tueddiad ag enghreifftiau eraill. Na, gall lefel effeithlonrwydd y dulliau uchod amrywio'n sylweddol, yn dibynnu ar y math penodol o swyddogaeth y bydd y llinell duedd yn cael ei hadeiladu ar ei chyfer. Felly, os yw'r dull a ddewiswyd yn fwyaf effeithiol ar gyfer y swyddogaeth hon, nid yw hyn yn golygu o gwbl y bydd hefyd yn optimaidd mewn sefyllfa arall.

Os na allwch eto benderfynu ar unwaith, yn seiliedig ar yr argymhellion uchod, pa fath o frasamcan sy'n addas yn benodol ar gyfer eich achos, yna mae'n gwneud synnwyr rhoi cynnig ar yr holl ddulliau. Ar ôl adeiladu llinell duedd a gweld ei lefel hyder, bydd yn bosibl dewis yr opsiwn gorau.

Send